Decision Forest Regressor
랜덤 포레스트 회귀는 결정트리를 앙상블한 모델로, 이전의 선형이나 다항 회귀 모델과 달리
개별 선형 함수의 합으로 이해할 수 있다.
결정 트리 알고리즘으로 압력 공간을 학습하기 좋은 더 작은 영역으로 분할한다.
결정 트리는 비선형 데이터를 다룰 때, 특성 변환이 필요없다.
결정 트리는 가중치가 적용된 특성 조합을 고려하는 것이 아닌, 한 번에 하나의 특성만 평가
(결정 트리는 특성 정규화나 표준화가 필요없다.)
정보이득이 최대화하는 특성 분할을 찾는 것이 목표이다.
(자식 노드에서 불순도가 최대로 감소되는 특성 분할)
분류에서 불순도 지표로 지니불순도, 엔트로피, 분류오차를 사용했다.
회귀에서는 결정 트리를 사용하려면, 연속적인 특성에 적합한 불순도 지표가 필요하기 때문에
MSE를 노드 t의 불순도 지표로 정의한다.
결정트리에서는 MSE를 노드 내 분산(within-node variance)라고 한다.
따라서 분할 기준을 분산 감소(variance reduction)라고 한다.
from sklearn.tree import DecisionTreeRegressor
X=df[['LSTAT']].values
y=df['MEDV'].values
tree=DecisionTreeRegressor(max_depth=3)
tree.fit(X, y)
sort_idx=X.flatten().argsort()
lin_regplot(X[sort_idx], y[sort_idx], tree)
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000s [MEDV]')
plt.show()
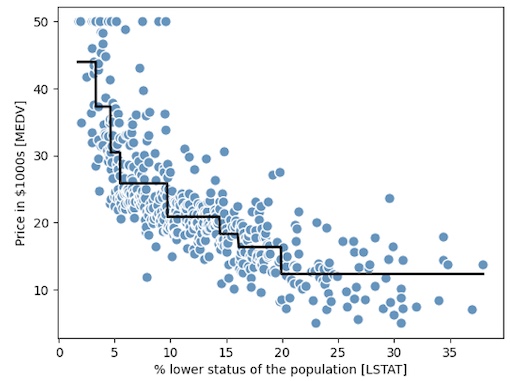
그래프에서 알 수 있듯이, 결정트리는 데이터에 있는 일반적인 경향을 잡아낸다.
기대하는 예측이 연속적이고 매끄러운 경우를 나타내지 못하는 한계가 있다.
또한 과대적합, 과소적합되지 않도록 적절한 크기의 깊이를 주의 깊게 선택해야 한다.
Random Forest Regressor
여러개의 결정 트리를 연결하는 앙상블 방법이 랜덤 포레스트 알고리즘이다.
랜덤 포레스트는 무작위성이 모델의 분산을 낮추어 주기 때문에 일반적으로 단일 결정 트리보다 더 나은 일반화 성능을 낸다.
랜덤 포레스트는 데이터셋에 있는 이상치에 덜 민감하고 하이퍼파라미터 튜닝이 많이 필요하지 않다는 장점이 있다.
(유일한 하이퍼파라미터는 앙상블의 트리 개수이다.)
분류를 위한 랜덤 포레스트 알고리즘과 트리 성장을 위해 MSE를 기준으로 사용한다는 점을 제외하고는 동일하다.
타깃 값의 예측은 모든 결정 트리의 예측을 평균하여 계산한다.
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
X=df.iloc[:, :-1].values
y=df['MEDV'].values
X_train, X_test, y_train, y_test=train_test_split(X, y, test_size=0.4, random_state=1)
from sklearn.ensemble import RandomForestRegressor
forest=RandomForestRegressor(n_estimators=1000, criterion='mse', random_state=1, n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred=forest.predict(X_train)
y_test_pred=forest.predict(X_test)
print('훈련 MSE: %.3f, 테스트 MSE: %.3f' %(mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('훈련 R^2: %.3f, 테스트 R^2: %.3f' %(r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
훈련 MSE: 1.644, 테스트 MSE: 11.085
훈련 R^2: 0.979, 테스트 R^2: 0.877
과대적합이 된 경향이 있지만, 여전히 타깃과 특성간의 관계를 잘 설명해 준다.
plt.scatter(y_train, y_train_pred-y_train, c='steelblue', edgecolor='white', marker='o', s=35, alpha=0.9, label='Training data')
plt.scatter(y_test_pred, y_test_pred-y_test, c='limegreen', edgecolor='white', marker='s', s=35, alpha=0.9, label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='black')
plt.xlim([-10, 50])
plt.tight_layout()
plt.show()
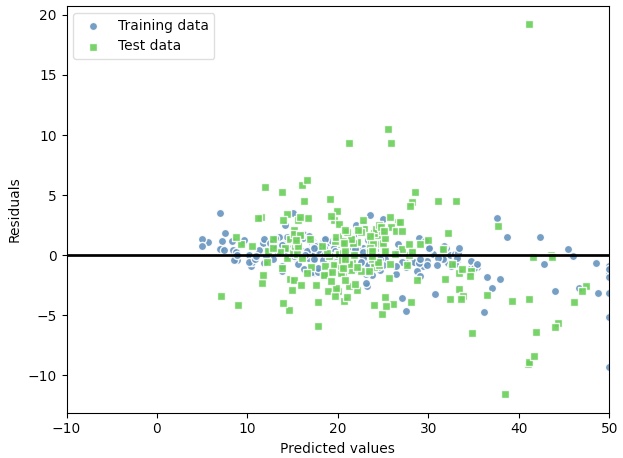
이상적으로 모델의 오차가 랜덤하거나 예측할 수 없어야 한다.(예측 오차가 특성에 담긴 어떤 정보와도 관계가 없어야 한다.)
현실 세계에 있는 분포나 패턴의 무작위성
잔차 그래프를 조사하여 예측 오차에 패턴이 감지된다면 잔차 그래프가 예측 정보를 담고 있다는 의미이다.
일반적으로 특성의 정보가 잔차로 누설된 것이다.
랜덤하지 않는 잔차 그래프 문제를 다루기 위한 보편적인 방법이 없기 때문에 실험을 해 보아야만 한다.
가용데이터에 따라 특성을 변환하거나 학습 알고리즘의 하이퍼파라미터를 튜닝하여 모델을 향상시킬 수 있다.
또는 더 간단하거나 더 복잡한 모델을 선택할 수 있고, 이상치를 제거하거나 추가적인 특성을 포함하여 모델의 성능을 높일 수 있다.
Random Tree in classify & regression
Random Tree는 기본적으로 정보 이득(IG)이 최대화 되는 특성 분할을 결정한다.
분류 모델에서는 연속적인 특성이 아니기 때문에 불순도 지표로 지니 불순도와 엔트로피 등을 사용했지만,
(자식 노드에서 불순도가 최대로 감소되는 분할)
회귀 모델에서는 연속적인 특성에 대한 불순도 지표가 필요하다. MSE를 불순도 지표로 사용할 수 있다.
(노드 내 분산 MSE가 최대로 감소되는 분할)